
Varje kvadratisk matris \(A\) är associerad med ett tal kallat matrisens determinant, betecknad \(\det{A}\) eller \(|A|\), som kan avslöja många egenskaper hos matrisen. Inom kursens ram talar vi nästan aldrig om vad en determinant definitionsmässigt är, utan mer om hur en determinant kan beräknas och tolkas.
Sats: Om \(A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\) gäller \[\det{A} = ad - bc\] Formeln ovan kan även illustreras med följande diagram:

Sats: Om \(A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix}\) gäller \[\begin{aligned} \det{A} &= a_{11}a_{22}a_{33} +a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\ &-\,a_{31}a_{22}a_{13} - a_{32}a_{23}a_{11} -a_{33}a_{21}a_{12}\end{aligned}\] Formeln ovan kan även illustreras med följande diagram:
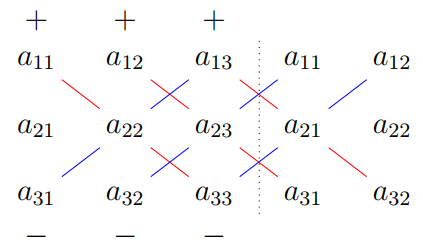
Anmärkning: Satsen kallas även Sarrus regel, efter den franske matematikern Pierre Frédéric Sarrus (1798-1861). Varning: Samma diagramkonstruktion får inte tillämpas för att beräkna determinanten av en godtycklig kvadratisk matris av storlek \(4 \times 4\) eller högre.
Generellt kan determinanten av en \(n \times n\)-matris \(A\) beräknas hjälp av Laplaces kofaktorutveckling längs en valfri rad eller valfri kolonn i \(A\). Utvecklingen är uppkallad efter den franske matematikern Pierre-Simon Laplace (1749-1827).
För att kunna formulera en kofaktorutveckling behöver vi först lära oss begreppen minor och kofaktor.
Minor: Minoren \(M_{ij}\) till \(A\) är determinanten av den delmatris som erhålls efter att rad \(i\) och kolonn \(j\) tagits ur \(A\).
Kofaktor: Kofaktorn \(C_{ij}\) motsvarande minoren \(M_{ij}\) ges av \[C_{ij} = (-1)^{i+j} M_{ij}\] En minnesregel är att tecknet som ges av \((-1)^{i+j}\) finns i positionen (rad \(i\), kolonn \(j\)) i ”schackbrädesmatrisen” \[\begin{bmatrix} + & - & + & - & + & \cdots \\ - & + & - & + & - & \cdots \\ + & - & + & - & + & \cdots \\ - & + & - & + & - & \cdots \\ + & - & + & - & + & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{bmatrix}\] Sats: Determinanten av en \(n \times n\)-matris \(A\) beräknas genom att kofaktorutveckla längs en valfri rad eller valfri kolonn i \(A\).
Längs rad \(i\): \[\det{A} = \sum_{k=1}^{n} a_{ik}\,C_{ik} = a_{i1} \,C_{i1} + a_{i2} \,C_{i2} + \cdots + a_{i2} \,C_{i2}\] Längs kolonn \(j\): \[\det{A} = \sum_{k=1}^{n} a_{kj}\,C_{kj} = a_{1j} \,C_{1j} + a_{2j} \,C_{2j} + \cdots + a_{2j} \,C_{2j}\]
Populära genvägar: Med hjälp av kofaktorutveckling kan vi få följande trevliga resultat:
1. Om \(A\) har en nollrad eller nollkolonn, gäller \[\det{A} = 0\] 2. Om \(A\) är en triangulär matris, gäller \[\det{A} = \text{produkten av huvuddiagonalelementen}\] (Påminnelse: Om kvadratisk matris sägs vara triangulär om alla element nedanför eller alla element ovanför huvuddiagonalen är \(0\).)
För att underlätta bestämningen av en determinant kan lämpliga radoperationer göras, för att få in många nollelement i matrisen, innan en kofaktorutveckling utförs. Tre viktiga regler:
1. Om \(B\) fås genom att addera en multipel av en rad med en annan rad i \(A\): \[\det{A} = \det{B}\] 2. Om \(B\) fås genom att låta exakt två rader i \(A\) byta plats med varandra: \[\det{A} = - \det{B}\] 3. Om \(B\) fås genom att multiplicera en hel rad i \(A\) med ett tal \(k \neq 0\): \[\det{A} = \frac{1}{k} \det{B}\] Anmärkning: Eftersom \(\det{A^T} = \det{A}\) för alla \(n \times n\)-matriser \(A\), kan även liknande kolonnoperationer göras.
Följande gäller för alla \(n \times n\)-matriser \(A\), \(B\) och alla tal \(k \in \mathbb{R}\).
1. Multiplikativitet: \(\quad \det{(AB)} = \det{A} \cdot \det{B}\)
(Det finns däremot ingen generell och samtidigt enkel regel för \(\det{(A+B)}\).)
2. Invarians under transponering: \(\det{A^T} = \det{A}\)
3. Matrisinvers: \(\displaystyle{\det{A^{-1}} = \frac{1}{\det{A}}}\)
(om \(A\) är inverterbar)
4. Multiplikation med skalär: \(\det{(kA)} = k^n\,\det{A}\)
(observera exponenten \(n\))
Tam Vu
för 6 år sedan